ВЕРШИНА ДЕЯТЕЛЬНОСТИ РЕГИОМОНТАНА(начало статьи - «Начало деятельности Региомонтана»)
Региомонтан, получив в Вене от короля Матиаса Корвина, разрешение на строительство обсерватории и типографии, в скором времени реализует свои намерения. В 1471 году прибыв в Нюрнберг, он закладывает фундамент для строительства обсерватории и типографии. Известно, что при закладке и строительстве обсерватории использовал чертежи восточных архитекторов и методы их строительство. В 1475 году Региомонтан направляется в Рим по приглашению Римского папы Сигестина VI для работы над календарем, спустя год умирает там. По некоторым предположениям он был убит, либо скончался от холеры. Во времена Региомонтан астрономы применяли инструменты, заимствованные у арабов, а то и у древних греков астролябии, трикветры (параллактические линейки), армиллы, квадранты, «градштоки» или «якобштабы» («посохи Якова»), а для измерения времени различные разновидности солнечных, звездных, а так же лунных часов. Интерес к астрономическим инструментам пробудился у Региомонтана в самом начале его деятельности. Имеются сведения, что уже около 1455 г. oн написал сочинение об «альбионе» - сложном астрономическом приборе, имитирующем движения небесных тел, который был изобретен Ричардом из Валингфорда в 1327 г. Сочинение Региомонтана об этом приборе до нас не дошло, неизвестно, занимался ли он его изготовлением. К 1457 г. относится работа Региомонтана о «геометрическом квадрате» («Quadratum geometricum»). Этот прибор применялся в землемерии еще в XI в., впервые был описан французским ученым Жаном Линьером в 1322 г.  Календарь составленный Региомонтаном
Примерно в то же время Региомонтан описал прибор «Instrumente namussis» («точный инструмент»), предназначенный для измерения высот Солнца и звезд. Тогда же Региомонтан занялся и совершенствованием дорожных часов. В Нюрнберге хранится образец астролябии, изготовленный Региомонтаном в 1468 г. из латуни. Диаметр прибора 280 мм. на тимпане изображена стереографическая проекция кругов небесной сферы для широты 500, примерно на полградуса отличающейся от широты Нюрнберга. Альмукантараты проведены через два градуса. Своеобразны очертания «паука», напоминающие ствол дерева с ветвями. На них нанесены положения 18 северных звезд, расположенных внутри круга эклиптики, и 13 южных, внешних. У некоторых звезд указана их звездная величина. Существуют и другие астролябии, сделанные лично Региомонтаном или под его руководством в мастерской в Нюрнберге. Для всех них характерно одно: сменные тимпаны на широты 390-420 (Южная Италия, Рим), 450-480 (Северная Италия, почти вся Франция, Южная Германия, Швейцария, Австрия, Венгрия) и 510-540 (Южная Англия, Голландия, Северная Германия, Польша). Около 1465 г. он составляет для кардинала Виссариона руководство к использованию разработанной им разновидности армиллярной сферы, которую ученый называет «Meteoros copiumannulare» («армиллярным метеороскопом») 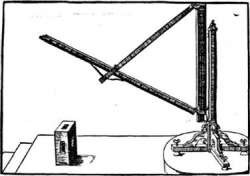 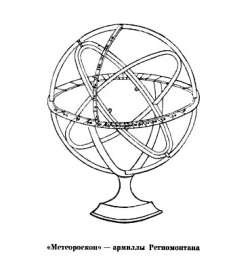 Трикветрум Армиллярный метеороскоп
В метеороскопе неподвижными являются отградуированные меридианный и горизонтальный круги, внутри которых вокруг полюса мира вращаются круг склонения и экваториальный круг. Зенит меридианного круга соединен с горизонтальным кругом дугой в 900, так же отградуированной. На круге склонения имеются два визира для наблюдений. Прибор предназначался так же для решения такой географической задачи, как нахождение долготы и широты некоторого места, если даны его расстояние и азимутальный угол относительно другого места с известной долготой и широтой. Руководство Региомонтана было издано Й. Вернером в 1514 г. в его сборнике «In hoс operе continentur» вместе с изображением инструмента, которое здесь приводится, затем в книге «Introductio Geographiсe Petri Apiani…» («Введение в географию Петра Апиана …») и в третий раз – в сборнике майнцского врача и любителя астрономии Дриандера: «Annulorum tri um diversi generis instrument!» («Об инструменте, образованном тремя различными кольцами»). Уже после смерти Региомонтана его нюрнбегский ученик Б. Вальтер построил армиллярную сферу и использовал ее в наблюдениях с 1488-1504 гг. В 1512-1541 гг. с помощью армилл проводил наблюдения Н. Коперник. Различные усовершенствованные конструкции армилл были созданы и широко применялись Тихо Браге.2 Несмотря на рано оборвавшуюся жизнь Региомонтан перевел на латинский язык «Сферику» Менелая и «Шары» Теодосия и др. труды. Здесь хочу коснуться одной интересной детали. Произведение александрийца Менелая «Сферика» не дошло до наших дней. Но уже в раннем средневековье Абу Несир ибн Ираги перевел этот труд на арабский язык. Вероятнее всего, Региомонтан видел этот перевод, имеется ввиду арабский вариант. Потому, что привел данные из этого труда в своем знаменитом трактате о роли плоскостной и сферической тригонометрии в астрономии и математике под названием «Joanis Regio Montanus De triaquius pianis et sphericis lidev v. unae cürtabulus sinum». Это произведение было завершено им в 1464 г. во время пребывания в Италии, где он занимался переводами старинных манускриптов. Однако, труд был напечатан лишь спустя 69 лет, т.е. в 1533 г. удивительно, как Региомонтану удавалось заниматься одновременно переводами и подготовкой самостоятельной научной работы. В апреле 1464 года Региомонтан прибывает в Падую, где знакомится с Дж. Бьянкини. Здесь читает лекции в Падуанском Университете по истории математики и о творчестве Альфрагануса (аль-Фергани). Определенный вклад в тригонометрию был сделан также испано-арабским математиком Джабиром ибн Афлахом, работавшим в Севилье в середине XII веке (в латинских текстах его имя часто переводится как Гебер, Geber). Он впервые в Европе получил решение сферического треугольника по данному катету и противолежащему углу (правило Гебера). Результаты тригонометрических работ ученых стран ислама и их предшественников, были в значительной мере обобщены в «Снятии покрывала с тайн фигуры секущих» или «Трактате о полном четырехугольнике» Туси, относящемся к 1260 г. В истории математики трактат Туси считается первым сочинением, в котором тригонометрия рассматривается как, самостоятельный раздел математики, а не как вспомогательный аппарат для решения астрономических задач.  Джабир ибн Афлах (Гебер) (721-815)
Писатель-исследователь Рамиз Дениз
Президентский стипендиат по литературе,
лауреат премии «Золотой перо».
email: [email protected], [email protected] 2 Белый Ю. А. Тихо Браге. М. «Наука», 1982. стр. 229
 24942 24942 |
|








 AZ
AZ EN
EN RU
RU